GCLMTP

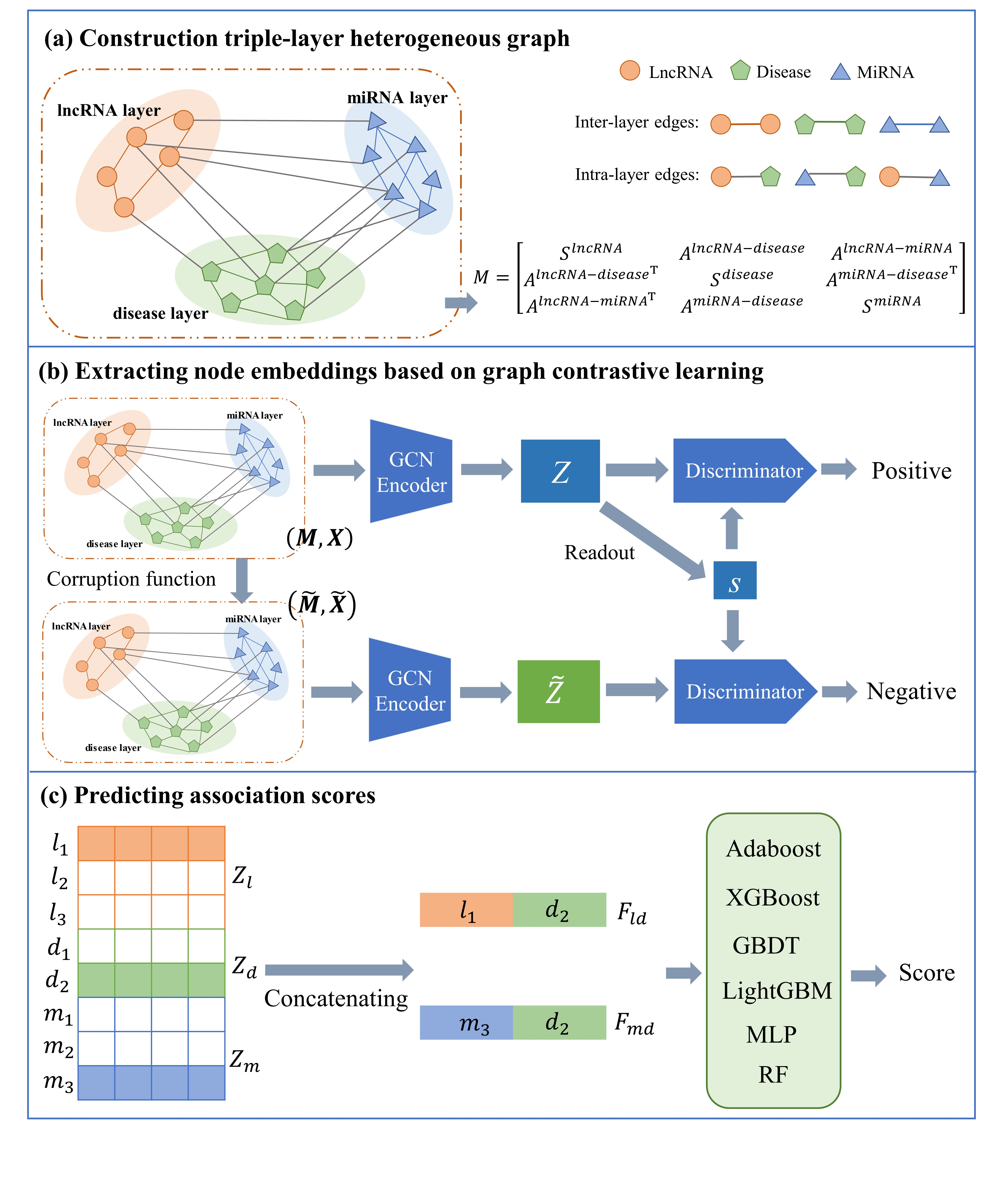
矩阵操作

def read_file1():
    # 加载 lncRNA 和 miRNA 之间的关联数据
    lnc_mi = np.loadtxt("data/yuguoxian_lnc_mi.txt")
  
    # 将 lncRNA 和 miRNA 之间的关联数据转置，表示 miRNA 和 lncRNA 之间的关联数据
    mi_lnc = lnc_mi.T
  
    # 加载 lncRNA 与疾病之间的关联数据
    lnc_dis = np.loadtxt("data/lnc_dis_association.txt")
  
    # 加载 miRNA 与疾病之间的关联数据
    mi_dis = np.loadtxt("data/mi_dis.txt")
  
    # 加载疾病之间的相似性数据
    dis_sim = np.loadtxt("data/dis_fusion_sim.txt")
  
    # 加载 lncRNA 之间的相似性数据
    lnc_sim = np.loadtxt("data/lnc_fusion_sim.txt")
  
    # 加载 miRNA 之间的相似性数据
    mi_sim = np.loadtxt("data/mi_fusion_sim.txt")
  
    # 加载 lncRNA 与疾病关联数据的测试标识符
    lnc_dis_test_id = np.loadtxt("data/lnc_dis_test_id1.txt")
  
    # 加载 miRNA 与疾病关联数据的测试标识符
    mi_dis_test_id = np.loadtxt("data/mi_dis_test_id1.txt")
  
    # 加载 miRNA 和 lncRNA 之间关联数据的测试标识符
    mi_lnc_test_id = np.loadtxt("data/mi_lnc_test_id1.txt")
  
    # 返回加载的数据作为函数的输出
    return mi_lnc, lnc_dis, mi_dis, dis_sim, lnc_sim, mi_sim, lnc_dis_test_id, mi_dis_test_id, mi_lnc_test_id

以上代码形状为 (495, 240) (240, 405) (495, 405) (405, 405) (240, 240) (495, 495) (95051, 2) (189628, 2) (117999, 2)，test为在矩阵中为即将在copyA中置零的矩阵

def Preproces_Data(A, test_id):
    copy_A = A / 1
    for i in range(test_id.shape[0]):
        copy_A[int(test_id[i][0])][int(test_id[i][1])] = 0
    return copy_A

程序中对lnc疾病、mi疾病、lncmi做了如上处理，后续 matrix_A = construct_graph(lnc_dis, mi_dis, mi_lnc, lnc_sim, mi_sim, dis_sim)，把上面三个矩阵构造进去，同时也把三个变量自己之间相关性也包含在内。

然后依照这个先做hstack，再做vstack。我发现处理数据时，lncRNA与miRNA顺序是反过来的，所以我修改了代码。将其先做转置，再更改

def construct_graph(lncRNA_disease, miRNA_disease, lncRNA_miRNA, lncRNA_sim,
                    miRNA_sim, disease_sim):
    lnc_dis_sim = np.hstack((lncRNA_sim, lncRNA_disease, lncRNA_miRNA))
    print(lnc_dis_sim.shape)
    dis_lnc_sim = np.hstack((lncRNA_disease.T, disease_sim, miRNA_disease.T))
    print(dis_lnc_sim.shape)
    mi_lnc_dis = np.hstack((lncRNA_miRNA.T, miRNA_disease, miRNA_sim))
    print(mi_lnc_dis.shape)
    matrix_A = np.vstack((lnc_dis_sim, dis_lnc_sim, mi_lnc_dis))
    return matrix_A

拉普拉斯归一化

def lalacians_norm(adj):
    # adj += np.eye(adj.shape[0])
    degree = np.array(adj.sum(1))
    D = []
    for i in range(len(degree)):
        if degree[i] != 0:
            de = np.power(degree[i], -0.5)
            D.append(de)
        else:
            D.append(0)
    degree = np.diag(np.array(D))
    norm_A = degree.dot(adj).dot(degree)
    return norm_A

GCNConv

GCNConv 是一个自定义的 PyTorch 模块类，继承了 nn.Module。这表示它是一个可训练的神经网络层，可以包含可学习的参数。
在初始化方法 __init__ 中，定义了 GCNConv 层的参数：
- in_size 表示输入特征的维度大小，即节点特征的数量。
- out_size 表示输出特征的维度大小，即经过该层后节点特征的维度。
在 __init__ 中，创建了一个可训练的权重矩阵 self.weight 作为 GCNConv 层的参数。这个权重矩阵的大小是 (in_size, out_size)，初始化使用 Xavier 初始化方法，以确保参数的初始值是合适的，有助于网络的训练。
在 forward 方法中，定义了 GCNConv 层的前向传播操作：
- adj 是图的邻接矩阵（Adjacency Matrix），表示节点之间的连接关系。
- features 是节点的特征矩阵，表示每个节点的特征向量。
在前向传播中，首先执行 torch.mm(adj, features) 操作，将邻接矩阵 adj 与特征矩阵 features 相乘。这个操作相当于对每个节点的特征与其邻居节点的特征进行聚合，得到了节点聚合后的特征表示。
然后，执行 torch.mm(out, self.weight) 操作，将上一步得到的聚合特征矩阵与 GCNConv 层的权重矩阵 self.weight 相乘。这个操作实现了将聚合后的特征进一步映射到输出特征空间，得到了最终的输出特征表示。
最后，将计算得到的输出特征 out 返回作为这个 GCNConv 层的输出。

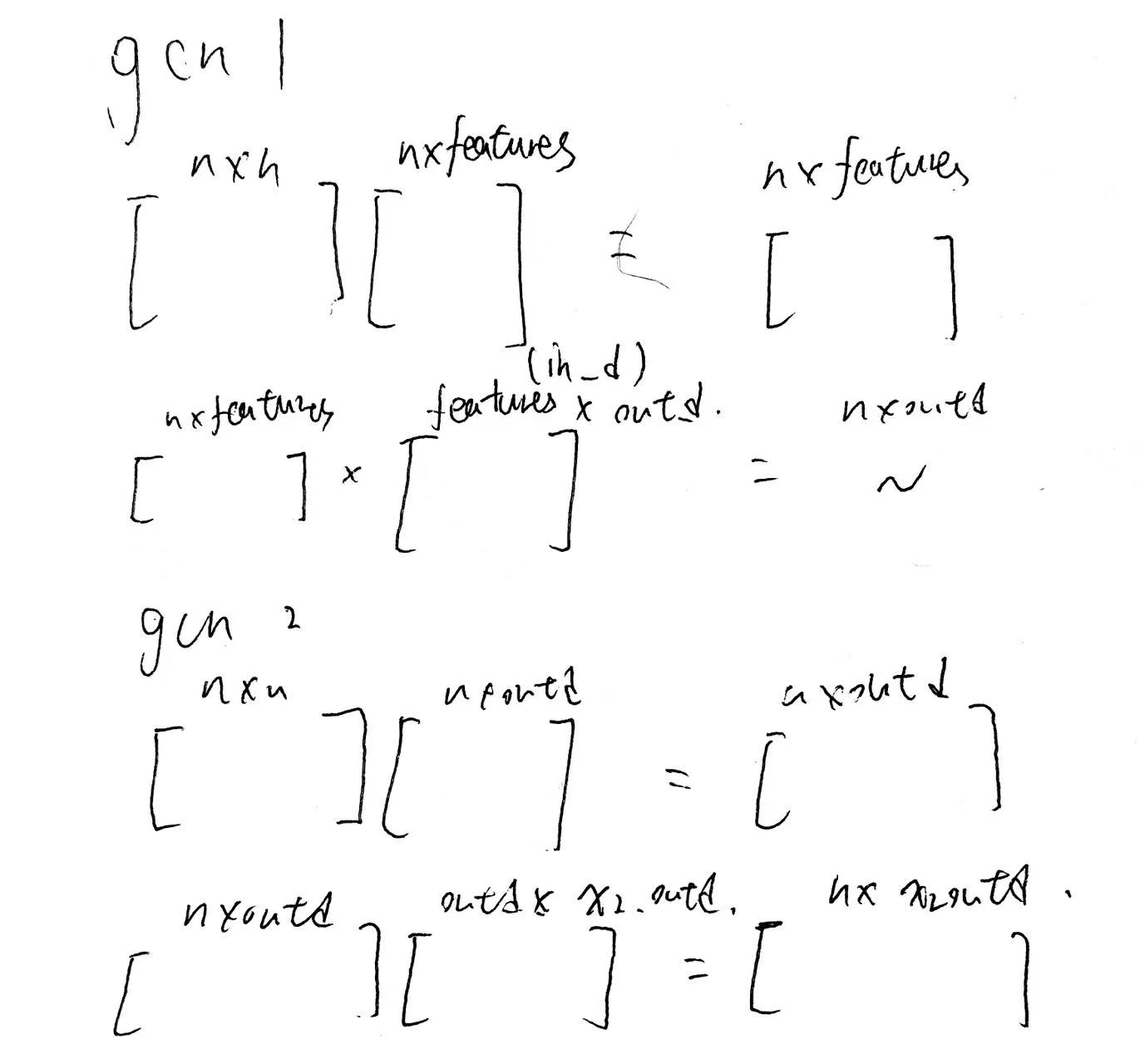
图为encoder的一种结构

Encoder

## input_dim是输入的维度，hidden_dim是隐藏层的维度，n_calss是输出的维度
class Encoder(nn.Module):

    def __init__(self, input_dim, hidden_dim, n_calss):
        super(Encoder, self).__init__()
        self.gcn1 = GCNConv(input_dim, hidden_dim)
        self.prelu1 = nn.PReLU(hidden_dim)

        self.gcn2 = GCNConv(hidden_dim, n_calss)
        self.prelu2 = nn.PReLU(n_calss)

        self.last_linear = torch.nn.Linear(hidden_dim + n_calss, n_calss)

    def forward(self, x, adj, corrupt=True):
        if corrupt:
            perm = torch.randperm(x.shape[0])
            x = x[perm]

        x1 = self.gcn1(adj, x)
        x1 = self.prelu1(x1)
        x2 = self.gcn2(adj, x1)
        x2 = self.prelu2(x2)

        return x2

不再赘述

模型本身

GCLMTP是一个基于图的模型，它利用编码器从输入数据生成正样本和负样本，然后使用判别器进行处理，并根据判别器的输出计算损失。这个模型的目的似乎是在图结构的数据上进行未监督的学习，可能是用于图嵌入或者相似的任务。

Corrupt

## hidden_dim是隐藏层的维度
# discriminator是一个全连接层，输入是hidden_dim，输出是hidden_dim
class Discriminator(nn.Module):

    def __init__(self, hidden_dim):
        super(Discriminator, self).__init__()
        self.weight = nn.Parameter(torch.Tensor(hidden_dim, hidden_dim))
        nn.init.xavier_uniform_(self.weight.data, gain=1.414)

    def forward(self, x, summary):
        x = torch.matmul(x, torch.matmul(self.weight, summary))
        return x


'''Model'''


class GCLMTP(nn.Module):

    def __init__(self, input_dim, hidden_dim, output_dim):
        super(GCLMTP, self).__init__()
        self.encoder = Encoder(input_dim, hidden_dim, output_dim)
        self.discriminator = Discriminator(output_dim)
        self.loss = nn.BCEWithLogitsLoss()

    def forward(self, edge_index, x):
        positive = self.encoder(x, edge_index, corrupt=False)
        negative = self.encoder(x, edge_index, corrupt=True)

        summary = torch.sigmoid(positive.mean(dim=0))

        # print("summary: ",summary.shape)
        positive_D = self.discriminator(positive, summary)
        negative_D = self.discriminator(negative, summary)

        l1 = self.loss(positive_D, torch.ones_like(positive_D))
        l2 = self.loss(negative_D, torch.zeros_like(negative_D))

        L = l1 + l2
        return L, positive

代码的核心在于 positive = self.encoder(x, edge_index, corrupt=False),corrupt代表是否生成错误特征，这也是对比学习的一个特点。

positive是通过编码器处理输入数据得到的“正”样本的输出，其形状应该是 [N, output_dim]，接下来的 positive.mean(dim=0)计算了 positive沿第0维度（即沿样本数方向）的平均值。这会得到一个长度为 output_dim的向量，其每个元素表示所有样本在该特定维度上的平均值。torch.sigmoid函数被应用于这个平均值向量。sigmoid函数将任何输入压缩到0和1之间。这意味着 summary是一个介于0和1之间的值的向量，表示所有正样本的平均特征。

Discriminator

Discriminator接受两个输入：x和 summary。x是从编码器得到的输出，是正样本或负样本的表示，而 summary是前面提到的正样本的平均特征。torch.matmul(self.weight, summary)是一个矩阵与向量的乘法操作，它实际上是在为每个特征维度提供一个权重，这些权重来自 self.weight。然后得到的结果与输入 x再次进行矩阵乘法。这是将 x的每个样本与通过 summary加权的权重进行相乘。

我认为判别器实际上是在使用 summary 来影响或加权它如何处理输入的样本。

summary = torch.sigmoid(positive.mean(dim=0))

>>> positive:  torch.Size([1140, 256])
summary:  torch.Size([256])

可以看出，dim进行了降维度。

这样，判别器实际上是在使用 summary（即正样本的平均特征）来影响或加权它如何处理输入的样本。

从高级角度看，Discriminator的目的是判断一个给定的样本表示（x）与整体“正”样本分布（由 summary表示）有多接近。如果 x表示的样本接近于正样本分布，那么判别器的输出会更接近1（正类），否则它会更接近0（负类）。

训练

def train(la_A, Epoch, in_features, N_HID, out_features, LR):

    G = GCLMTP(input_dim=in_features,
               hidden_dim=N_HID,
               output_dim=out_features)
    G_optimizer = torch.optim.Adam(G.parameters(), lr=LR)
    A_laplacians = torch.from_numpy(la_A).float()
    X = torch.from_numpy(la_A).float()
    # print(A_laplacians.shape,X.shape)
    ################################GPU#############################
    if torch.cuda.is_available():
        G = G.cuda()

        A_laplacians = A_laplacians.cuda()
        X = X.cuda()

    ###########################model train###########################
    for epoch in range(Epoch):
        G_loss, embedding = G(A_laplacians, X)

        G_optimizer.zero_grad()
        G_loss.backward()
        G_optimizer.step()
        print('Epoch: ', epoch, '| train G_loss: %.10f' % G_loss.item())
    np.savetxt("dataset1_result/low_A_256.txt",
               embedding.detach().cpu().numpy())

训练过程比较常规，无需单独记录

疑问

       A_laplacians = A_laplacians.cuda()
       X = X.cuda()

G_loss, embedding = G(A_laplacians, X)

代码中 X矩阵即为经过拉普拉斯正则化的 matrix_A ，但我们发现作为 edge_index的矩阵仍是 matrix_A

我推测是因为这个矩阵中包含了足够多的特征